Qu’est-ce que la géométrie sacrée ?
La géométrie sacrée est une géométrie utilisée par les architectes et les artistes pour créer leurs œuvres.
La géométrie sacrée peut être définie comme un ensemble de proportions, de manipulations géométriques
et de dimensions, telles qu’elles ont pu être observées dans la nature. Les cristaux, les fleurs, les fruits, les animaux,
tous ont servi de modèle pour cette géométrie. La nature étant considérée comme une perfection,
l’être humain peut en comprendre les lois d’organisation géométrique et s’en inspirer pour ses propres créations.
C’est pour cette raison qu’elle est appelée géométrie sacrée. A l’origine, cette recherche avait pour but de démontrer l’existence d’un dieu ayant créé le l’univers et tout ce qu’il contient selon des plans établis grâce à la géométrie. Cette recherche n’a jamais permis d’en démontrer l’existence, Les règles établies pour cette géométrie ont servi pendant des siècle pour créer de manière cohérence et symbolique à défaut d’assurer la beauté.
Elle est encore employée de nos jours par certaines personnes recherchant la perfection dans leurs créations.

Tracé géométrique obtenu en reliant les fosses de calage des menhirs, tracé inscrit dans un carré barlong
l’angle est d’une telle précision, qu’il est difficile d’imaginer que cela soit le fruit du hasard.
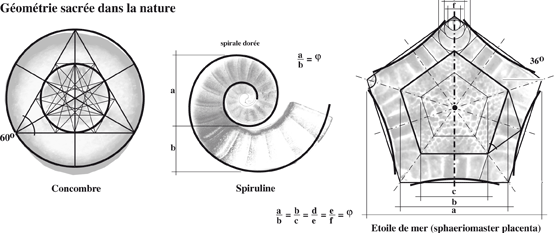
Les formes géométriques sont très nombreuses dans la nature, que ce soit dans des structures infiniment petites jusqu’aux plus grandes.
Cependant, il ne faut pas non plus voir de la géométrie Là où il n’y en a pas. Le Nautile n’est pas sur le nombre d’or, sauf dans de très rares cas !
Géométrie sacrée dans les flocons de neige
les proportions les plus courantes sont basées sur la racine de 3 (normal vu la forme hexagonales des cristaux) et sur la racine de 2. Ces proportions servent à définir les hexagones homothétiques et concentriques qui sont à la base du tracé régulateur. Ces hexagones et la prolongation des côtés définit chaque départ de ramure ou sa taille maximale.

A quoi sert la géométrie sacrée ?
Le but de la géométrie sacrée est de créer de la cohérence et de l’harmonie. C’est un outil de création qui permet de ne rien laisser au hasard, de tout justifier par les proportions et de générer de l’ordre. Chaque élément, aussi petit soit-il, est toujours en rapport avec le tout. Même si ce n’est pas prouvé scinetifiquement, je suis convaincu qu’elle favorise le bien-être et peut-être même la santé. La géométrie sacrée est une discipline de l’esprit favorisant l’élargissement de la conscience.
Subjectif me direz-vous ? Pas tant que cela, avec des machines quantiques comme le GDV ou le LVA, il est maintenant possible de montrer l’impact de la géométrie sacrée sur le rayonnement électrophotonique émis par le corps. En résumé : plus d’ordre, plus d’énergie, plus de potentiel d’évolution, plus de conscience.
Quels sont les domaines d’application de la géométrie sacrée ?
Principalement dans les édifices religieux, mais aussi dans tous les bâtiments construits par les maîtres bâtisseurs : château, tombeau, hospice, mausolée, pyramide, pont, etc. Elle a été appliquée depuis la nuit des temps. C’est à la Renaissance que les principes mathématiques ont été mis en place pour expliquer les tracés géométriques. Auparavent, la géométrie utilisait principalement le carré et sa diagonale. Les nombres irrationnels tels que Phi ou Pi n’existent que depuis pas très longtemps, mais on les trouvent indirectement par le jeu des tracés géométrique, utilisant juste la règle et le compas.
Pour avoir étudié les tracés géométriques d’édifices de toutes les époques et de toutes les cultures, je peux affirmer qu’elle est présente partout et de tout temps. Quelques exemples seront donnés plus loin.
Quelles sont les caractéristiques de la géométrie sacrée ?
Tout d’abord, l’utilisation de proportions bien précises et en nombre limité :
• les proportions basées sur les rapports musicaux
• les proportions basées sur le nombre d’or
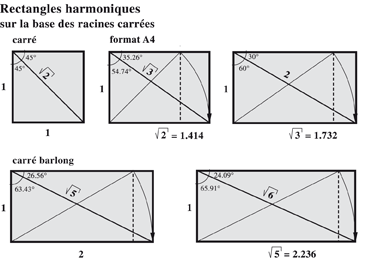
• les proportions basées sur les racines carrées
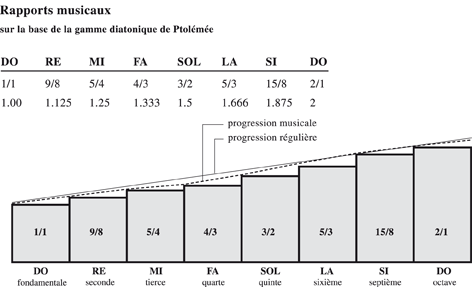
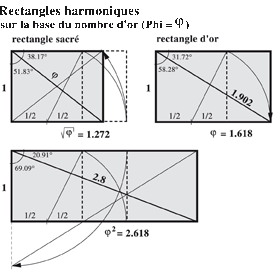
Ensuite, une série de manipulations géométriques, telles que :
• l’homothétie
• la rotation
• la symétrie
• l’inscription
• la division sacrée ou dorée
• la décomposition et la juxtaposition
La bissection est une combinaison de l’homothétie et de la rotation
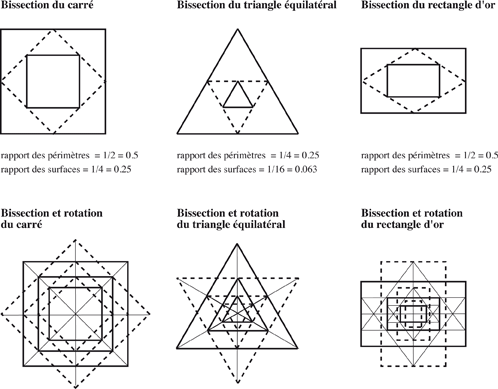


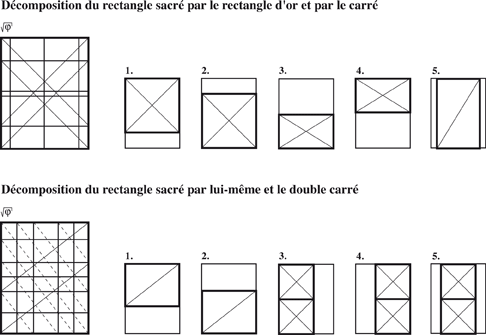
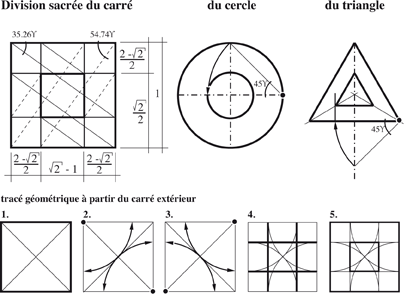
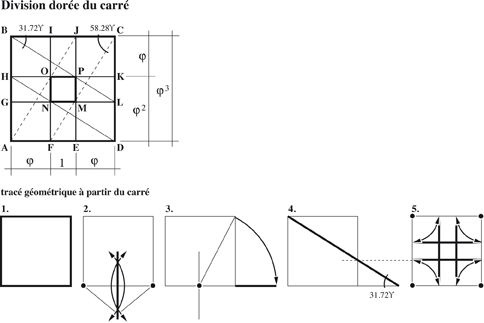
Et des formes géométriques parfaites, comme :
• le carré
• le triangle équilatéral
• le cercle
• le rectangle d’or
• le pentagone
• l’hexagone
• l’octogone
Enfin, un système de mesures permettant de passer du plan à la réalisation :
• le mètre (égyptien, néolithique, etc.)
• la coudée (royale, locale, sacrée, etc.)
• le pied (romain, de Charlemagne, etc.)
• le pouce
Les unités de mesures sont nombreuses et ont souvent varié au cours des âges. Ainsi la coudée égyptienne n’a pas toujours eu la même longeur.
Les anciens utilisaient principalement des nombres entiers, car le nombre entier était considéré comme une perfection en soi.
Le pied romain
Le pied romain de 29.5cm, comme la plupart des unités de mesure de l’Antiquité, sont basées sur le déplacement des soldats en colonne de marche sur une route. En ce qui concerne les Romains, tout est basé sur le double pas de 147.5cm (une moyenne pour une troupe). En divisant le double pas par 5, nous obtenons 29.5cm. Le double pas de 5 pieds fut utilisé jusqu’au 18e siècle, avec des pieds variables d’une région à l’autre. Parmi toutes les absurdités entendues, le pied romain ne vient pas de la pointure d’un empereur (ce seraitdu 46, un peu grand pour des Romains !), ni de la durée du mois lunaire (aucun rapport entre une unité de mesure de la distance et du temps).
Les 3 tables
Selon la tradition des bâtisseurs, trois tables ont porté le Graal, l’une est ronde, l’autre est carrée et la dernière est rectangulaire, toutes ont la même surface et leur nombre est 21. Ce nombre n’a rien à voir avec le rectangle de proportion 2/1 (carré barlong), si c’était le cas les bâtisseurs auraient dit « leur proportion est 21 ». En réalité, il s’agit d’une astuce de bâtisseur s’adressant à ceux qui ont la connaissance, c’est-à-dire appris le grec ancien. Le nombre 21 fait référence à la 21ème lettre de l’alphabet grec, la lettre Phi, soit le nombre d’or ! Le nombre d’or (plus précisément, la racine 4e du nombre d’or) sert à définir le rapport entre le diamètre d’un cercle et le côté d’un carré ayant tous les deux la même surface. Par calcul, il est facile de constater que
le résultat est précis à 0.4 pour mille près ! Je me suis toujours demandé comment ils avaient réussi à faire ces calculs. Ci-dessous, voici comment le tracé de cette quadrature surfacique peut être obtenue en la dessinant au moyen de la corde à 13 noeuds, à partir de nombres entiers, en l’occurence le triangle 3-4-5 fort prisé par les Anciens.

Les bâtisseurs ont eu recours aux nombres et à leur symbolique.

Quels étaient les outils pour tracer un plan ?
Les seuls outils étaient la règle, l’équerre et le compas. La règle sert à tirer des traits droits, l’équerre à tracer des angles et le compas à dessiner des cercles. Ceux qui prétendent avoir trouvé le tracé régulateur d’un édifice ancien en utilisant d’autres outils que la règle, l’équerre et le compas sont dans l’erreur. Le but d’un tracé régulateur est de définir tous les éléments de la constructions, donc en priorité les murs, les colonnes et les ouvertures. La priorité est donnée au tracé des murs extérieurs (nu du mur extérieur), à l’épaisseur de ces murs, puis aux murs intérieurs et aux ouvertures. Pour les édifices à colonnes, tout le tracé permet de définir les axes des colonnes. Actuellement, les logiciels d’architectes procèdent toujours de la même manière.
Un tracé régulateur sert uniquement à définir tous les éléments de la construction, pas à y cacher des soi-disant connaissances ésotériques.

Comment reporter un plan sur le terrain ?
La première opération est de tracer sur le terrain les axes principaux du bâtiment. On choisit un point, en général un point de croisement important des réseaux telluriques. Les axes sont définis par la direction donnée par lesdits réseaux. La personne qui avait la compétence pour le faire n’était que rarement l’architecte, souvent un chaman ou un druide, un initié aux énergies telluriques. Cette connaissance était également transmise par l’oral, elle a existé dans toutes les cultures, dans toutes les époques depuis 6000 ans. En Europe continentale, elle a disparu en grande partie vers 1350, définitivement vers 1695. La géobiologie l’a remise au goût du jour dès le début du 20e siècle.
Relation entre la géométrie sacrée, le tellurisme et l’astronomie
Le recours aux réseaux telluriques est systématique dans toute l’histoire de l’humanité, dès les premières constructions, comme on peut encore le ressentir de nos jours dans les sites mégalithiques. Conjointement au respect du tellurisme local, certaines pierres étaient placées selon des angles en relation avec les levers et couchers de soleil aux solstices ou aux équinoxes, ou encore les levers et couchers extrêmes de lune tous les 9,3 ou 18,6 ans. Voici un exemple, à Avebury, le célèbre site mégalithique en Angleterre

Comme la direction des réseaux telluriques dépend de la géologie, les édifices suivent toujours les courbes de niveaux. Ceci explique que chaque église ait sa propre orientation ; il n’y a aucun rapport avec une orientation basée sur des soi-disant levers de soleil le jour du saint patron de l’église. En dehors de la période néolithique, les bâtisseurs n’ont pas eu recours à l’astronomie pour définir le lieu pour implanter leurs édifices, contrairement à ce que certains prétendent.
Comment reporter une distance ?
Pour tracer le bâtiment sur le terrain, les bâtisseurs utilisaient une ficelle enduite de craie et une canne (perche en bois de 2 à 5m de long) pour reporter des distances. L’avantage du bois est qu’il ne varie que très peu dans le sens de la longueur, ceci assure une grande précision dans la mesure. De nos jours, ces outils sont encore utilisés dans la construction, la ficelle enduite de craie de couleur pour tracer des murs droits et le double mètre pliable pour mesurer des distances. Au début du 20e siècle, des cannes de 5m furent utilisées pour la construction du tunnel du Simplon, avant d’être détrônées par le laser. Un autre moyen pour reporter des distances sur le sol est d’employer une roue d’un diamètre précis. Cette méthode est toujours utilisée pour les métrés des routes.
Et la corde à 13 nœuds ?
Si une ficelle permet de tracer une ligne droite, elle ne peut en aucun cas être utilisée pour mesurer une distance, car son élasticité est telle qu’il n’est pas possible d’avoir une mesure fiable. La longueur d’une ficelle varie beaucoup trop avec l’humidité de l’air. Si, de surcroît, vous y ajouter des nœuds, c’est encore bien pire. La corde à 13 nœuds n’a donc jamais été utilisée pour reporter des mesures, par exemple, un certain nombre de coudées, mais elle a probablement servi pour l’instruction des apprentis en géométrie. Les nœuds étant pratiques pour visualiser des figures géométriques sans avoir à les tracer. Pourquoi 13 nœuds ? Parce que c’est le nombre d’intervalles nécessaires pour tracer la plupart des figures géométriques, en particulier le double carré (carré barlong), très cher aux bâtisseurs (13 nœuds = 12 intervalles = rectangle 2 / 4 / 2 / 4). Sur le plan symbolique, le 13, c’est aussi l’acte de se relier à l’Unité, à l’Absolu, à la Perfection du Créateur, le Grand Architecte
Comment reporter un plan sur le terrain ?
Un tracé sur place est fait de la même manière que le tracé sur la planche à dessin. On commence en général par le tracé hors tout (le périmètre dans lequel le bâtiment s’inscrit). Ceci permet d’obtenir une grande précision dans les mesures. Il est facile de comprendre que si l’on part du tout pour tracer ensuite les éléments plus petits, on évite les erreurs de mesures par addition de petits éléments. J’ai toujours été surpris de voir que la précision des bâtisseurs était incroyable, souvent en-dessous du pour mille !
Comment garantir l’horizontalité ?
Le moyen le plus simple pour garantir l’horizontalité d’un mur sur une grande distance est de creuser une rigole en fond de fouille est de la remplir d’eau additionnée de mortier ou de plâtre. Lorsque le mortier ou le plâtre se solidifie, on obtient un fond parfaitement horizontal. Pour des éléments plus petits, les bâtisseurs utilisaient aussi des niveaux à plomb.
Comment passer du plan à l’élévation ?
Pour garantir une unité dans les proportions, en général, la même proportion était utilisée pour le plan et le tracé des élévations et des coupes. Nous trouvons parfois des exceptions à cette règle, par exemple la racine de deux en plan et le nombre d’or en façade. La perfection est sans doute d’utiliser le même canevas géométrique pour les deux, mais les exemples sont plus rares. Sur le plan pratique, le fil à plomb permet de garantir la verticalité des murs.
Comment utiliser de nos jours la géométrie sacrée ?
En tant qu’architecte, j’ai eu recours de temps à autre à la géométrie sacrée. Il faut dire que dans ce métier les contraintes dimensionnelles sont très importantes. Tout est soumis à des normes (légales ou industrielles), il faut donc parfois faire des compromis. Le module des cuisines (60cm) n’est pas la coudée royale (52.36cm)! Tout construire sur mesure est faisable mais coûte hélas fort cher. L’accent est souvent mis sur les façades, car c’est là que les proportions sont les plus visibles. Dans mes ouvrages Géométries Sacrées, tomes 1 et 2, vous trouverez des centaines d’exemples d’édifices et d’objets réalisés avec la géométrie sacrée. Ils sont présentés avec leur tracé régulateur, dont un grand nombre permettant de les réaliser pas à pas.
Conclusion
J’espère que ce petit dossier vous a permis de mieux comprendre la géométrie sacrée, ses principes, son utilité, ses applications.
J’espère que vous regarderez dorénavant d’un autre œil les monuments que vous croisez. Et, qui le sait, peut-être aurez-vous envie d’appliquer la géométrie sacrée à vos réalisations. Pour ceux qui souhaitent davantage de détails, j’ai écrit des ouvrages et des dossiers sur différents sujets en lien avec la géométrie sacrée.
Exemples
Dans les planches qui suivent, j’ai essayé de vous montrer comment les anciens avaient tracé leurs œuvres.
Les exemples sont issus principalement de la culture occidentale, toutes époques confondues, par ordre chronologique.
Ce dossier s’agrandira au fur et à mesure de mes découvertes.
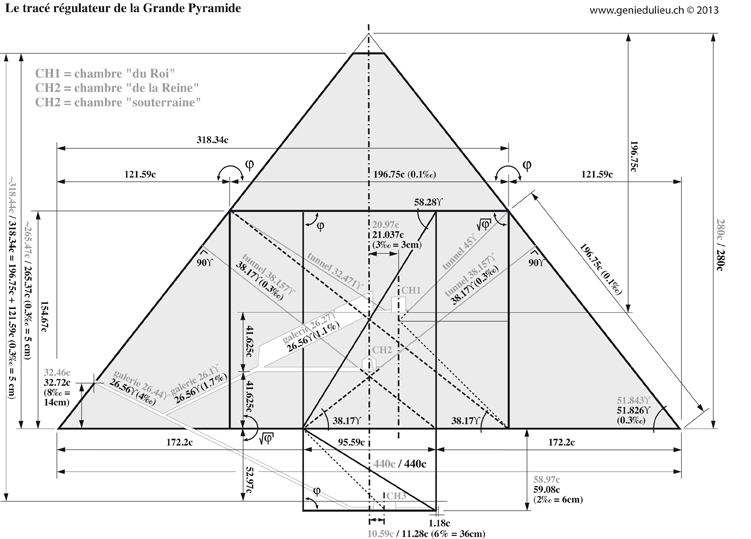
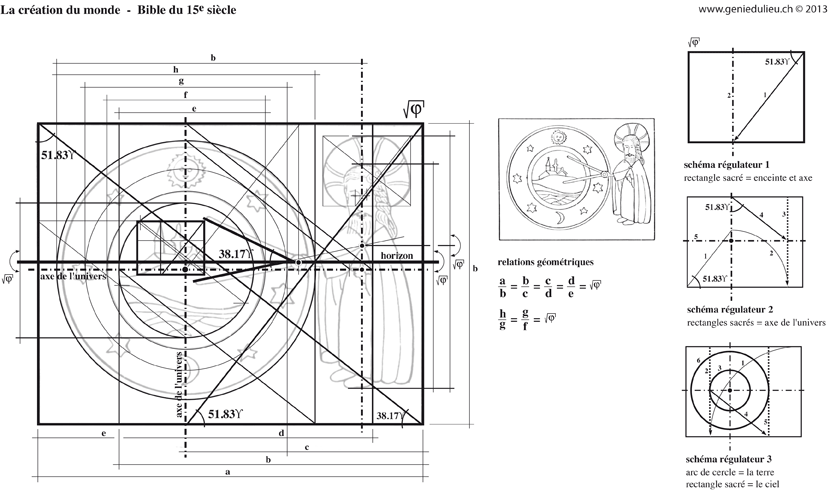
Le tracé géométrique de la Grande Pyramide est basé sur la racine du nombre d’or
Le « c » indique la coudée égyptienne de 52,36cm
La précision entre le tracé théorique et la mesure sur place est donnée en pour mille, souvent en-dessous du pour mille.
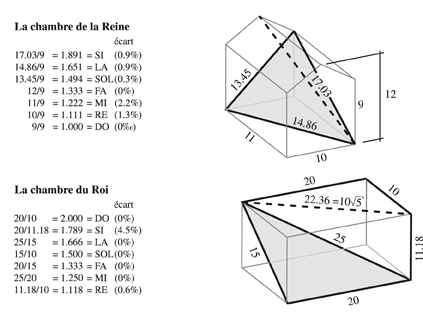
Les chambres de la Grande Pyramide sont basées sur les rapports musicaux avec une assez grande précision, de l’ordre du pour mille

Un exemple magnifique avec l’emploi systématique des rapports musicaux, inspiré par Pythagore

Un autre exemple basé sur les rapports musicaux, mais cette fois dans le monde romain
Notez la longueur hors tout en nombre entier (en centaines) de pieds romains
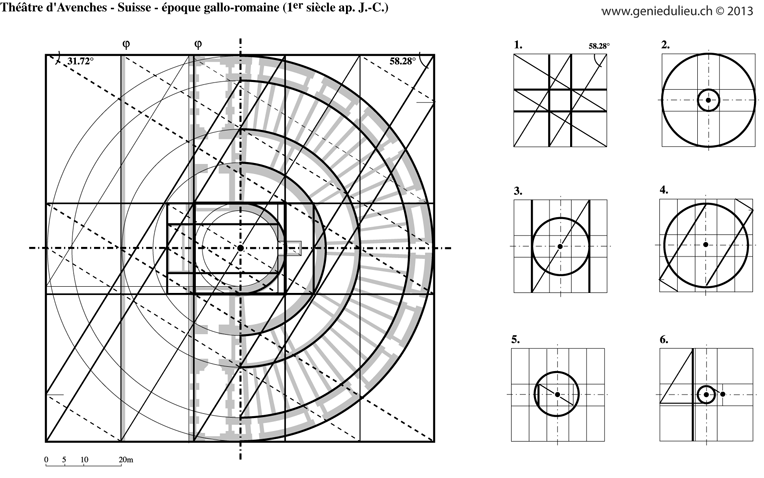
Utilisation du nombre d’or et surtout, de la division dorée pour les éléments principaux
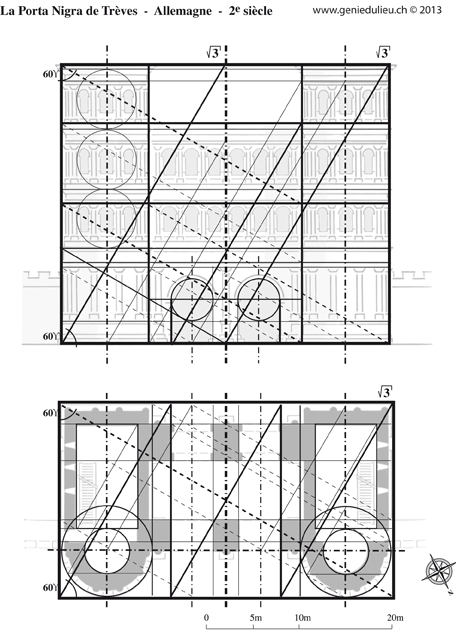
Utilisation de la racine de trois en plan et en élévation, des chefs-d’œuvre de l’art romain

Un monument colossal basé sur le nombre d’or, y compris pour l’extension bâtie sous Constantin
Quelques exemples dans l’art arménien, voir mon dossier sur l’architecture arménienne du 7e siècle.
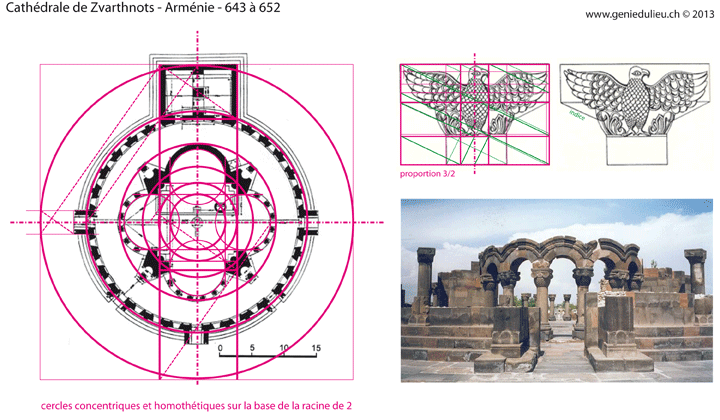
Une cathédrale de style bysantin, le successeur de l’art romain
Magnifique exemple d’homothétie basée sur la racine de deux
Sur le parchemin le plus vieux d’Angleterre
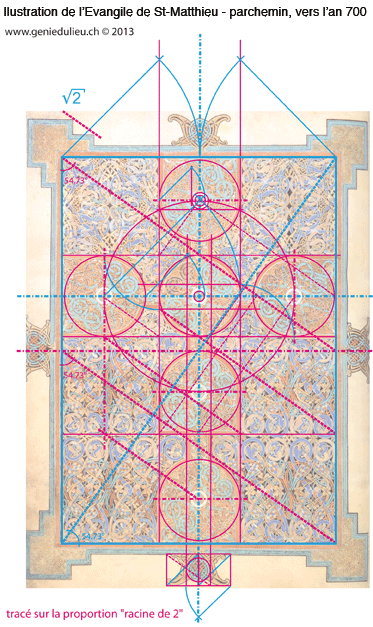
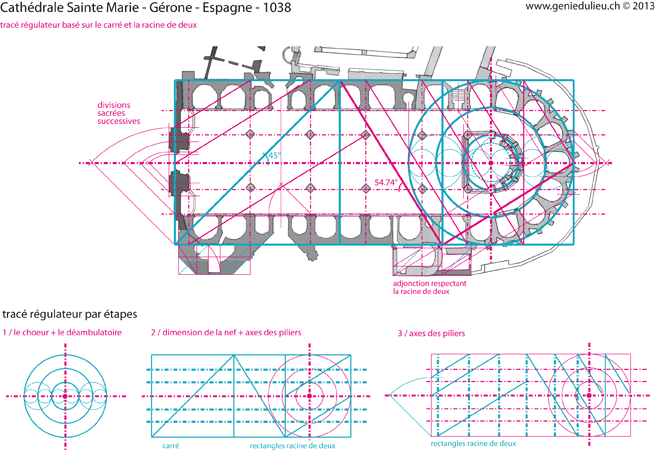
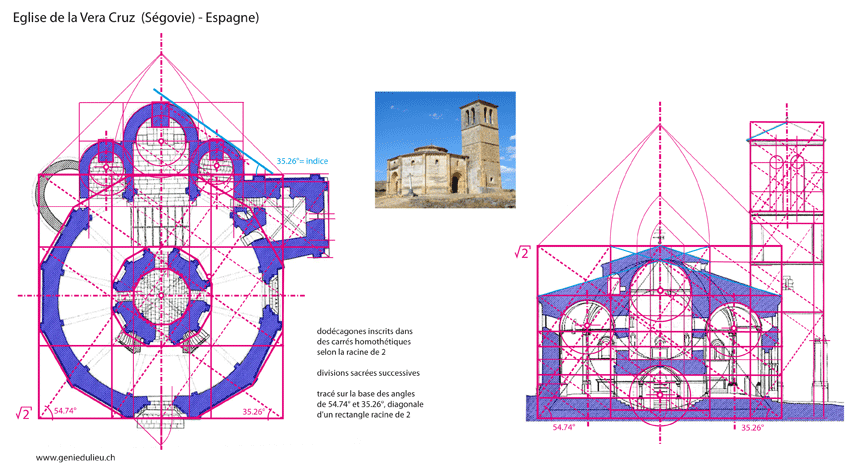
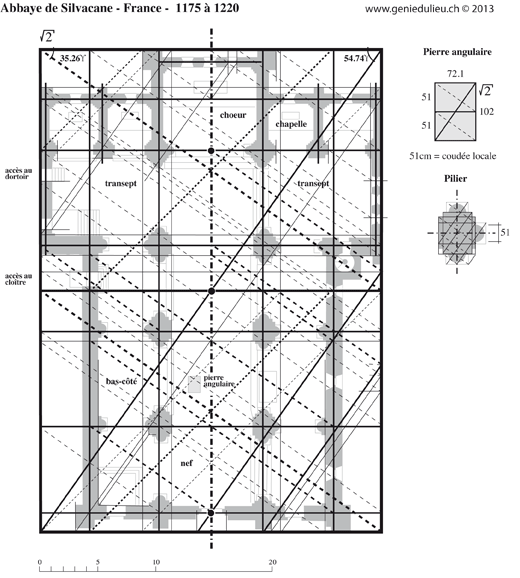
Plan inscrit dans un rectangle racine de deux / pierre angulaire combinant la coudée utilisée et l’angle de 35,26°
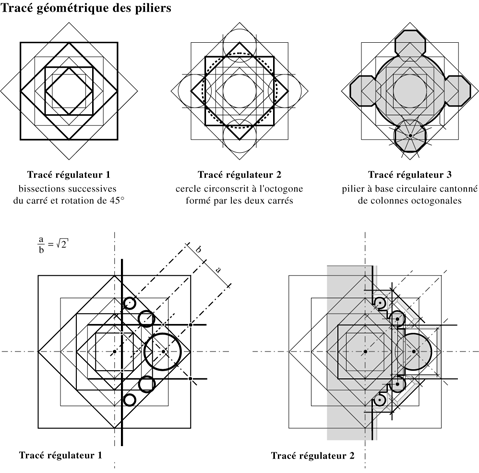
Tracé régulateur des piliers de la Cathédrale de Chartres, basé sur la bissection du carré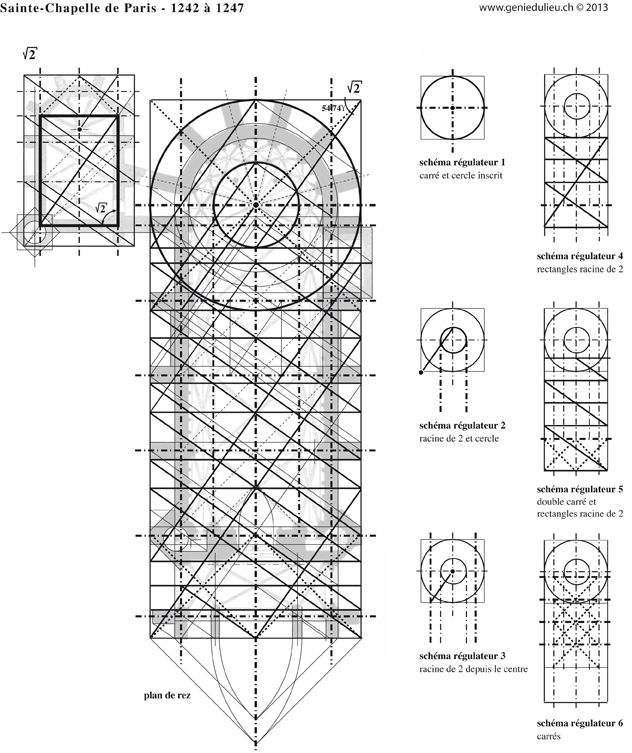
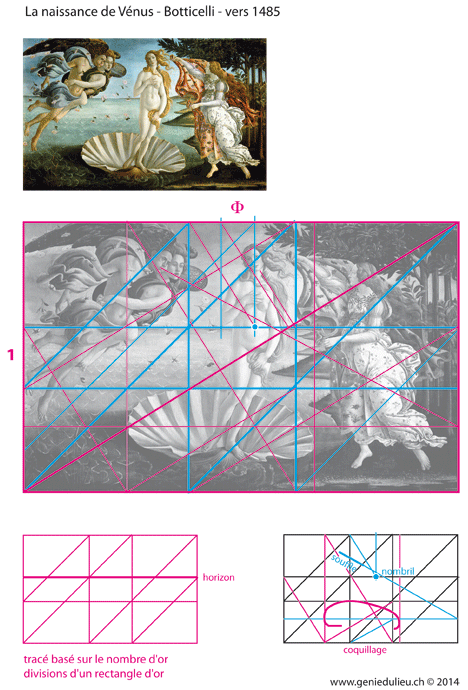
Voici deux exemples de tableau de la Renaissance, le procédé est toujours le même, subdivision du format du tableaupar les carrés collés à gauche et à droite, puis des diagonales pour définir les horizontales et verticales importantes
Un premier exemple basé sur la note LA. Notez l’effet de perspective, subtilement indiqué par l’angle du pinceau

Deuxième exemple, basé sur le nombre d’or, avec inscription de carrés et de rectangles d’or. L’artiste a utilisé le nombril de Vénus comme élément clé de la construction géométrique, il coïncide avec l’horizon et le bras de Vénus. Remarquez aussi les zéphyrs qui soufflent, la direction du souffle correspond exactement à la diagonale du rectangle d’or. Certains prétendent que la tableau a été raccourci en hauteur pour obtenir le nombre d’or.
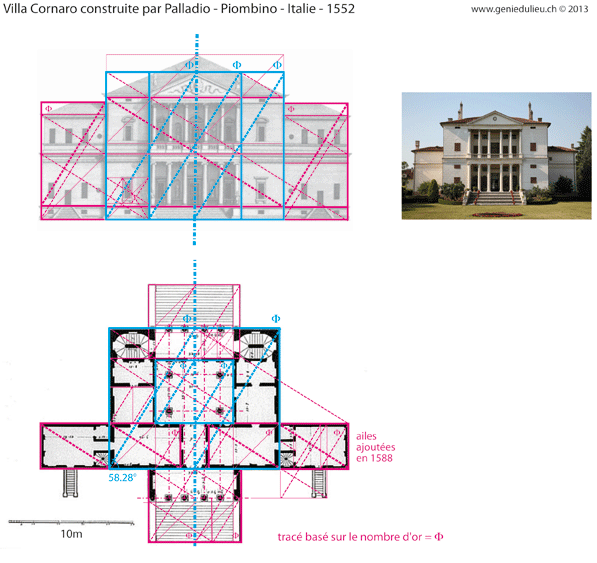
Remarquez la perfection du plan de Palladio. Son successeur a repris le nombre d’or pour son extension, mais avec maladresse, car les fenêtres ne s’harmonisent pas avec l’ancienne construction. Respecter une proportion ne garantit pas la beauté.

Dans le pur style de l’école des Beaux-Arts, basé sur la racine de trois et le carré, dans le moindre détail
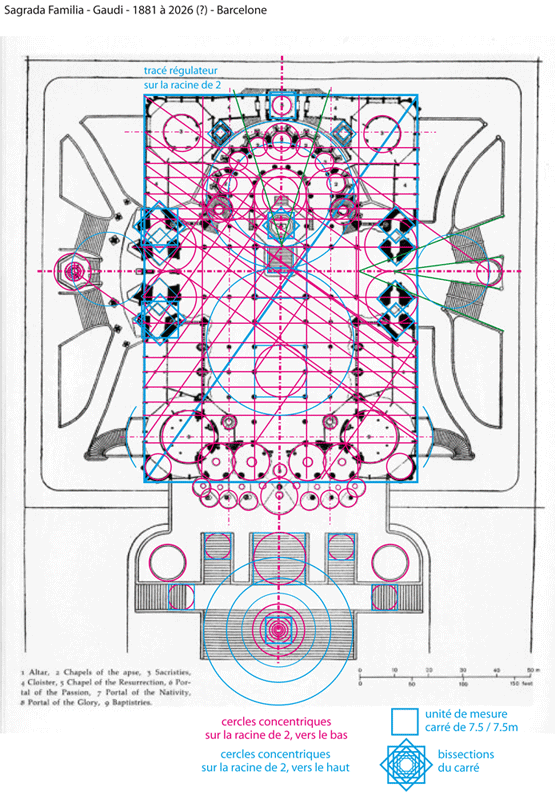
Dès 1881, l’architecte catalan Antonio Gaudi entreprend de dessiner et construire la célèbre Sagrada familia de Barcelone.
Il va utiliser des cercles concentriques basés sur la racine de 2, ainsi que des carrés circonscrits à ces cercles et la bissection:
Cette manière de tracer le plan d’une cathédrale est finalement assez classique et en droite ligne du Moyen Age. Elle combine un tracé sur la racine de deux, une modulation sur la base d’un module de 10 coudées, une inscription dans un rectangle racine de 2 et la très simple bissection de carrés. Nous avons là, un tracé d’une très grande cohérence car la bissection induit la racine de 2 et qu’en prenant la moitié d’une modulation revient à faire 2 x la racine de 2. La dimension du carré et du cercle de base est de 10 coudées locales (cosinus de la latitude de l’endroit), soit 0,75m avec une précision de 1 pour mille ! Ainsi Gaudi a obtenu le module qui a donné toutes les dimensions importantes. Toutes les tours ont une hauteur équivalent à un nombre entier de 10 coudées, ce qui fait un module de base de 7,5m, ainsi les trois tours principales font 17 x 7,5, 18 x 7,5 et 23 x 7,5 pour la plus haute, 172.5m.
Et finalement un exemple célèbre du 20e siècle, la Villa Savoie de Le Corbusier en 1928
une symphonie de carrés et de rectangles d’or, rien n’est laissé au hasard !